Red-black trees

binary search trees

1. 정렬된 binary trees 이다.
2. 각 노드는 2개의 subtree를 가진다. 이 subtree들도 binary search tree이다.
3. 주어진 노드 왼쪽 subtree의 모든 노드는 해당 노드보다 작은 값을 가진다.
4. 주어진 노드 오른쪽 subtree의 모든 노드는 해당 노드보다 큰 값을 가진다.

아래와 같은 모습을 지니며, 한쪽으로 몰리는 경우 탐색을 위해 O(n)의 복잡도를 가진다.

balanced search trees

위의 문제를 해결하는 구조이다. O(log n) 높이를 보장한다.

---

red-black tree

balanced search tree의 한 타입이다.

1. 모든 노드는 red 또는 black이다.
2. root 노드와 leaves 노드 (NIL)은 black이다.
3. red 노드의 자식은 항상 black이다.
4. 하위 NIL 까지의 모든 path에는 같은 수의 black 노드가 있다.

• 노드의 색을 저장하기 위한 1 bit 의 저장공간이 필요하다. 그래서 O(n)의 공간 복잡도를 가진다.
• root에서 NIL까지 가장 긴 path는 가장 짧은 path의 2배를 넘지 않는다.
  • shortest path : all black nodes
  • longest path : alternating red and black
• Search / Insert / Remove 3가지 동작이 있다.
• red-balck tree의 속성을 만족하기 위해 Insert, Remove는 ratation이 필요하다.
• 모두 O(log n)의 시간 복잡도를 가진다.

 

Rotations

• subtrees를 재배열하여 트리의 구조를 바꾼다.
• tree의 높이를 줄이는 것을 목표로 한다. 최대 목표는 위에서 말한 것 같이 O(log n)이다.
• 큰 sub trees를 위로 올리고, 작은 sub trees를 아래로 내린다.
• time complexity는 O(1)이다.
• rotation을 수행해도 red-black tree의 속성을 유지한다.

left-rotate & right-rotate

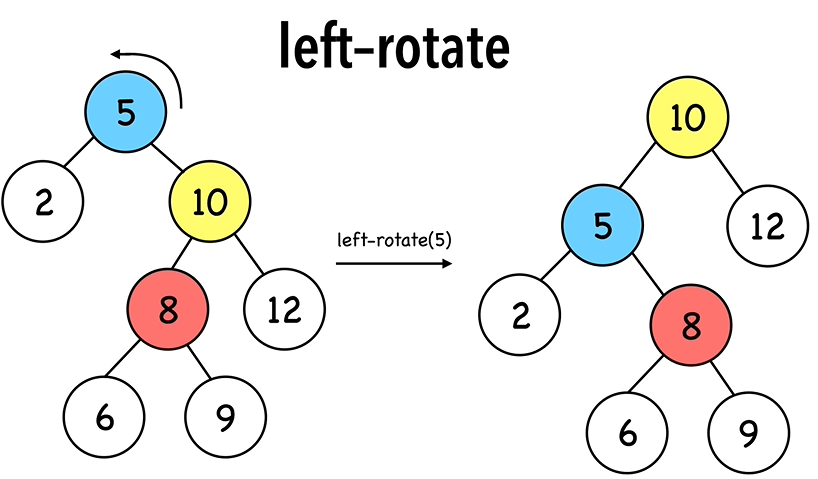
Insertions

1. red 인 Z 노드를 넣는다.
2. red-black tree 규칙에 맞게 색을 다시 칠하고 회전한다.

4가지 경우에 따라 동작이 다르다.

case 1) Z = root

red를 black으로 색만 바꾸면 된다. 

case 2) Z.uncle = red

부모, 조부모 노드의 색을 모두 바꿔준다.

case 3) Z.uncle = black (triangle)

Z.parent를 회전시킨다.

case 4) Z.uncle = black(line)

Z.grandparent 를 회전시키고, 기존 부모와 조부모의 색을 바꾼다.

Example

위의 전략을 사용하여, 아래의 상황에서 Insertion을 수행해보자.

 

먼저 아래에 tree에 10을 넣는다.

uncle이 red이기 때문에 case 2)에 맞게 색을 바꾼다.

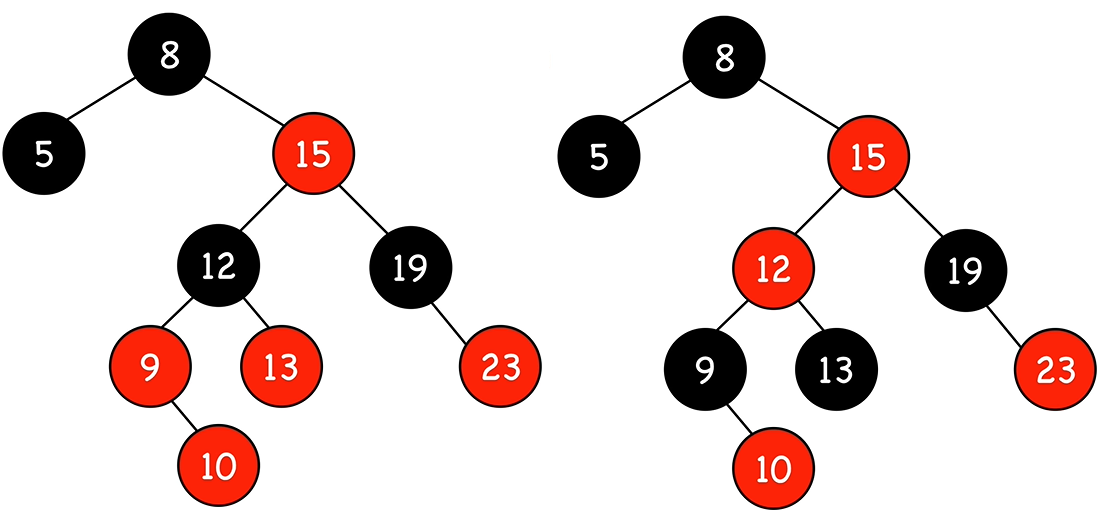
15 노드의 자식이 red일 수 없으므로 조건을 만족하지 않는다.

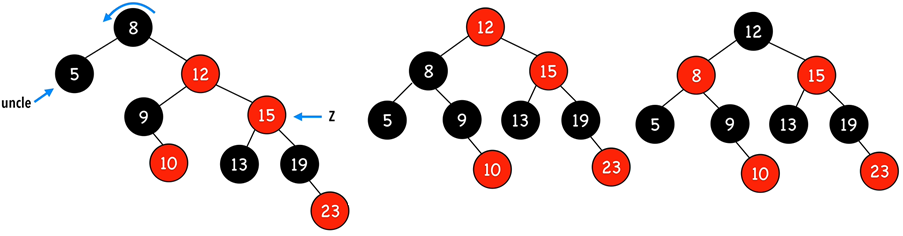
12가 z 노드가 되고, case 3)에 맞게 부모 노드를 회전시킨다.

12 노드 자식이 black이어야 하므로 조건을 만족하지 못한다.

15를 z노드로 하고 case 4)에 맞게 조부모 노드를 회전시킨다.

회전시킨 후 원래 부모와 조부모 노드의 색을 변경하면 red-black tree의 조건을 만족하면서 정렬된 tree가 된다.

time complexity

1. Insert : O(logn) / 어느 자리에 넣어야 하는지 대소 비교를 높이만큼 한다.
2. Color red : O(1)
3. Fix violations : O(logn)

결과적으로 Insertion을 수행하는데 복잡도는 O(logn) 이다.

---

https://youtu.be/qvZGUFHWChY